به نام آفریننده هستی
راهبردهای حل مساله
اهداف
- مجموعه ای از راهبردهای مناسب را در حل مسائل انتخاب کرده و بکار گیرند.
- فرآیند حل مساله ریاضی را بازبینی و کنترل نمایند و در آن بیندیشند.
- با دیگران بصورت منطقی و واضح در باره ی مسیر فکریشان گفتگو کنند.
روش تدریس
مسئله انبه در شکل شماره 1 مطرح شده است. قبل از مطالعه بقیه این طرح درس ، ابتدا مسئله را خوانده و به حل آن اقدام کنید. به چگونگی مراحل حل مسئله خود توجه نمایید. اگر گیج شده و موفق به حل نشدید ، در جستجوی راهبرد دیگری برای حل آن درآیید.
یک شب که پادشاهی از گرسنگی ، نتوانست بخوابد به آشپزخانه سلطنتی رفت و در آنجا ظرفی پر از انبه یافت. چون گرسنه بود 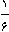 انبه ها را خورد و به اتاقش بازگشت. کمی بعد در همان شب ، ملکه نیز از شدت گرسنگی نتوانست بخواند . بنابراین او نیز در آشپزخانه ، انبه ها را یافت و انبه ها را خورد و به اتاقش بازگشت. کمی بعد در همان شب ، ملکه نیز از شدت گرسنگی نتوانست بخواند . بنابراین او نیز در آشپزخانه ، انبه ها را یافت و  انبه های باقیمانده را خورد. کمی بعد بزرگترین شاهزاده بیدار شد و انبه های باقیمانده را خورد. کمی بعد بزرگترین شاهزاده بیدار شد و  باقیمانده انبه ها را خورد.پس از او برادرش شاهزاده وسطی ، باقیمانده انبه ها را خورد.پس از او برادرش شاهزاده وسطی ، 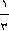 انبه های باقیمانده را خورد.سرانجام کوچکترین برادر انبه های باقیمانده را خورد.سرانجام کوچکترین برادر  انبه های باقیمانده را خورد . بدین ترتیب فقط 3 انبه برای خدمتکاران باقی ماند. در ابتدا چند انبه توی ظرف بود؟ انبه های باقیمانده را خورد . بدین ترتیب فقط 3 انبه برای خدمتکاران باقی ماند. در ابتدا چند انبه توی ظرف بود؟ |  |
مسئله انبه ، مورد علاقه معلمانی است که مایلند توانایی های حل مسئله را در دانش آموزانشان توسعه دهند. زیرا دانش آموزان راهنمایی می توانند این مسئله را حداقل از 4 راهبرد متفاوت حل نمایند.( راهبردهای حدس و آزمایش ، رسم شکل ، زیر مساله ، و تشکیل معادله ) این مسئله ، مثالی عالی برای نمایش قدرت و غنای ریاضی هنگام بکارگیری راهبردهای چندگانه در حل مسئله می باشد.
از این مسئله همچنین می توان برای اهداف آموزشی متنوع مانند ارزشیابی استفاده کرد در مواقعی که هدف ما از ارزشیابی ، توانایی دانش آموز در کاربرد راهبردهای متنوع باشد. همچنین با هدف استفاده از انواع راهبردها تا حد امکان ، از این مسئله می توان به عنوان تکلیف در کارگروهی مشارکتی بهره برد.
در مطالب زیر ، به هر یک از 4راهبرد مسئله انبه بصورت خلاصه می پردازیم همچنین تجربیات حاصل از اجرای عملی این راهبردها در کلاسها بیان می گردد ، دو تعمیم جالب برای مسئله پیشنهاد شده و مثالی از یک مسئله مشابه ( ملوان ها و نارگیل ها) در ادامه ی توسعه طرح درس برای بررسی بیشتر چهار راهبرد مذکور ، داده خواهد شد.
راهبرد حدس و آزمایش
در این راهبرد دانش آموزان ابتدا تعداد اولیه انبه های داخل ظرف قبل از ورود پادشاه به آشپزخانه را حدس می زنند سپس آنها برای بررسی حدس خود ، آن را با اطلاعات داده شده در مسئله می سنجند. اگر حدسشان درست نباشد ، بار دوم حدس بهتری را ( با استدلال منطقی ) مشخص می کنند. این فرآیند همچنان ادامه می یابد تا به پاسخ درست مسئله برسند . احتمالا برخی از دانش آموزان حدس هایی می زنند که غیرمعقول و نامربوط است .
در این موارد معلمان باید چگونگی آغاز یک حدس معقول را بدان ها خاطر نشان کنند و با آنها راجع به تشکیل جدولی برای ثبت و سازمان دهی اطلاعات مربوط به حدس های خویش ، صحبت نمایند.بدین ترتیب دانش آموزان براحتی از این راهبرد استفاده خواهند نمود.
تجربه عملی :
یکی از گروهها بسرعت فهمیدند که حدس اولیه آنها باید بر 6 قابل قسمت باشد تا پادشاه بتواند 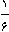 آن را بخورد و عدد 24 را به عنوان حدس اولیه بیان کردند اما در پایان مسئله 4 انبه به جای 3 انبه باقی ماند . بنابراین گروه فهمید که تعداد اولیه 24 انبه زیاد بوده و حدس خود را به عدد 18 اصلاح کرد . گروه با آزمایش عدد 18 فهمید که پاسخ صحیح مسئله است.
آن را بخورد و عدد 24 را به عنوان حدس اولیه بیان کردند اما در پایان مسئله 4 انبه به جای 3 انبه باقی ماند . بنابراین گروه فهمید که تعداد اولیه 24 انبه زیاد بوده و حدس خود را به عدد 18 اصلاح کرد . گروه با آزمایش عدد 18 فهمید که پاسخ صحیح مسئله است.
در گروه دیگری که آنها هم فهمیدند حدس اولیه باید بر 6 قابل قسمت باشد ، عدد 12 را پیشنهاد کردند. باآزمایش این عدد ، در پایان فقط 2 انبه باقی ماند. سپس انها به عدد بعدی قابل قسمت بر 6 یعنی 18 رسیدند.
برخی از گروهها درنیافتند که پاسخ باید بر 6 بخش پذیر باشد. آنها با حدس اعداد 16 و 14 نتوانستند بصورت دستی تقسیمات مسئله را انجام دهند و از ماشین حساب کمک گرفتند.
حدس اولیه یکی از گروهها 1000 بود که به 100 ، 30 ، 20 ، 19 و 18 اصلاح شد. آنها برای حدس اولیه خود از هیچ منطقی استفاده نکردند جز اینکه پس از آزمایش این حدس ، تعداد انبه های باقی مانده را بسیار زیاد یافتند.
راهبرد رسم شکل :
سهولت حل این مسئله با این راهبرد شگفت انگیز است. بدین منظور ابتدا مستطیلی رسم کنید که نشان دهنده تعداد اولیه انبه ها باشد . چون پادشاه 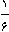 انبه ها را خورده است ، مستطیل را به 6 قسمت تقسیم کرده و 1 قسمت آن را حذف کنید.
انبه ها را خورده است ، مستطیل را به 6 قسمت تقسیم کرده و 1 قسمت آن را حذف کنید.

در اینصورت 5 قسمت مساوی باقی می ماند که ملکه 1 قسمت آن را خورده است. بنابراین 1 قسمت از 5 قسمت را هم حذف می کنیم.

به همین ترتیب  شکل باقی مانده را برای شاهزاده بزرگ
شکل باقی مانده را برای شاهزاده بزرگ

و 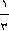 شکل باقی مانده را برای شاهزاده وسطی
شکل باقی مانده را برای شاهزاده وسطی
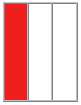
و  شکل باقی مانده را برای شاهزاده کوچکتر حذف می کنیم .
شکل باقی مانده را برای شاهزاده کوچکتر حذف می کنیم .

بدین ترتیب فقط 1 قسمت از مستطیل باقی می ماند که معادل 3 انبه می باشد .

اگر هر قسمت از مستطیل معادل 3 انبه باشد پس کل مستطیل یعنی تعداد اولیه انبه ها 18 خواهد شد. 18= 3×6
با این راهبرد بصورت تصویری و ملموس ، می توان مراحل حل مسئله را بخوبی نشان داد.
تجربه عملی :
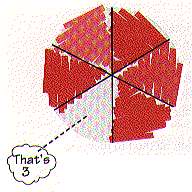
گروه دیگری نیز گرچه با روش مشابه حل کرد اما در پایان نتوانست با نسبت دادن عدد 3 به یک قسمت از دایره به پاسخ مسئله برسد و فقط عدد 3 را با تعداد قسمت های دایره یعنی 6 جمع کرد.
راهبرد زیر مساله :
استفاده از این راهبرد برای حل این مساله نه تنها برای دانش آموزان راهنمایی بلکه برای بزرگسالان هم آسان نیست. استفاده از این راهبرد مستلزم حل مساله از آخر به اول است. در این راهبرد ابتدا باید مساله را به چند مساله ی کوچک تقسیم کرد و مرحله به مرحله به حل آن پرداخت.
الف- ابتدا از انتهای مسئله شروع می کنیم( یعنی 3 انبه باقی مانده)
ب- بصورت برعکس مراحل مسئله را انجام می دهیم.
ج- با دقت مقدار هر مرحله را محاسبه می کنیم تا از انتها به ابتدای مسئله برسیم. برای مسئله انبه ها چنین انجام می دهیم :
- در انتهای مسئله 3 انبه باقی مانده بود که نشان دهنده
 انبه هایی بود که شاهزاده کوچک با آن مواجه شد. در اینصورت شاهزاده کوچک باید قبل از خوردن انبه ، 6 انبه دیده باشد.
انبه هایی بود که شاهزاده کوچک با آن مواجه شد. در اینصورت شاهزاده کوچک باید قبل از خوردن انبه ، 6 انبه دیده باشد. - تا این جا فهمیدیم وقتی شاهزاده وسطی
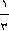 انبه ها را خورد 6 انبه باقی ماند. بنابراین 6 انبه معادل
انبه ها را خورد 6 انبه باقی ماند. بنابراین 6 انبه معادل 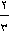 تعداد انبه ها بوده 9=
تعداد انبه ها بوده 9= × 6 پس قبل از اینکه شاهزاده وسطی انبه ای بخورد 9 انبه در ظرف بود.
× 6 پس قبل از اینکه شاهزاده وسطی انبه ای بخورد 9 انبه در ظرف بود. - بهمین ترتیب 9 انبه ، نشانگر
 انبه هایی است که شاهزاده بزرگتر با آن مواجه شد. پس 12=
انبه هایی است که شاهزاده بزرگتر با آن مواجه شد. پس 12= ×9
×9
قبل از اینکه شاهزاده بزرگتر انبه ای بخورد 12 انبه در ظرف بود.
- بطور مشابه می توان محاسبه کرد: 15=
 ×12 یعنی قبل از خوردن ملکه 15 انبه در ظرف بود.و
×12 یعنی قبل از خوردن ملکه 15 انبه در ظرف بود.و
18=
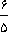 ×15 در ابتدا 18 انبه در ظرف موجود بوده است.
×15 در ابتدا 18 انبه در ظرف موجود بوده است.
تجربه عملی :
بعضی از دانش آموزان در انجام قسمت های 2 به بعد مشکل داشتند. برخی برای یافتن پاسخ هر مرحله ، از راهبرد حدس و آزمایش استفاده می کردند.
برخی این راهبرد را با راهبرد “ یافتن یک الگو“ ادغام کردند و وقتی در مراحل معکوس ، اعداد 3و 6 و9 را یافتند با الگوی ( هر دفعه 3 تا اضافه می شود ) به پاسخ 18 رسیدند.
برخی از دانش آموزان سه راهبرد “ زیر مساله “ “ رسم شکل “ و “ الگویابی “ را با هم ترکیب کردند. آنها ضمن رسم شکل ، الگوی افزایش سه تایی به اعداد را هم استفاده کردند. دانش آموزی که سریعتر از بقیه از این راهبرد به پاسخ صحیح رسید چنین استدلال می کرد:
6 نشان دهنده 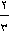 یک چیز است . پس
یک چیز است . پس 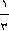 آن چیز باید 3 باشد پس اگر 6 (
آن چیز باید 3 باشد پس اگر 6 ( 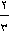 آن چیز ) را با 3 (
آن چیز ) را با 3 ( 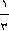 آن چیز ) جمع کنیم ، یعنی
آن چیز ) جمع کنیم ، یعنی  آن چیز را بدست آورده ایم.و بدین ترتیب به عدد 9 رسید.
آن چیز را بدست آورده ایم.و بدین ترتیب به عدد 9 رسید.
برای بدست آوردن عدد 12 از 9 چنین استدلال کرد: عدد 9 سه چهارم یک چیز است. اگر آن را به 3 تقسیم کنیم،  آن چیز بدست می آید، حال اگر 3 را با 9 جمع کنیم
آن چیز بدست می آید، حال اگر 3 را با 9 جمع کنیم 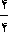 آن چیز بدست می آید.
آن چیز بدست می آید.
راهبرد تشکیل معادله :
برای دانش آموزان راهنمایی ، تشکیل معادله ای به منظور حل مسئله فوق ، بسیار دشوار است . برای تشکیل معادله ابتدا متغیر x را به تعداد اولیه انبه ها اختصاص می دهیم.
- چون پادشاه
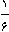 انبه ها را خورده پس مقدار باقیمانده آن برابر
انبه ها را خورده پس مقدار باقیمانده آن برابر 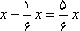 می گردد.
می گردد. - ملکه
 انبه های باقیمانده را خورد. پس از خوردن ملکه این مقدار باقی ماند :
انبه های باقیمانده را خورد. پس از خوردن ملکه این مقدار باقی ماند : 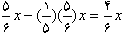
- شاهزاده بزرگتر
 انبه های باقیمانده را خورد یعنی مقدار باقیمانده برابر
انبه های باقیمانده را خورد یعنی مقدار باقیمانده برابر 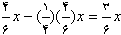 می گردد.
می گردد. - شاهزاده وسطی
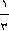 انبه های باقیمانده را خورد بنابراین
انبه های باقیمانده را خورد بنابراین 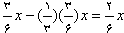 باقی می ماند.
باقی می ماند. - سرانجام شاهزاده کوچکتر
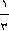 مقدار باقیمانده را خورد یعنی
مقدار باقیمانده را خورد یعنی 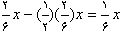 چون مقدار باقیمانده x
چون مقدار باقیمانده x 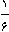 مساوی 3 می باشد پس 3= x
مساوی 3 می باشد پس 3= x 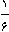 و 18= x
و 18= x
برای تمرین راهبردهای مطرح شده، می توان از مسئله زیر معروف به “ ملوانها و نارگیل ها “ نیز استفاده نمود.
  نارگیل های باقیمانده را برداشت و 1 نارگیل را برای میمون ها انداخت. صبح روز بعد ، ملوان ها متوجه شدند که کپه نارگیل ها خیلی کوچک شده ولی هر یک تصور می کرد که فقط او از نارگیل ها برداشته و بدین خاطر هیچکس حرفی نزد. آنها نارگیل های باقی مانده را به سه قسمت مساوی کردند و به هر یک 7 نارگیل رسید و 1 نارگیل هم اضافه آمد که ان را برای میمون ها انداختند. حال شما بگویید که در ابتدا ملوان ها چند نارگیل جمع آوری کردند؟ نارگیل های باقیمانده را برداشت و 1 نارگیل را برای میمون ها انداخت. صبح روز بعد ، ملوان ها متوجه شدند که کپه نارگیل ها خیلی کوچک شده ولی هر یک تصور می کرد که فقط او از نارگیل ها برداشته و بدین خاطر هیچکس حرفی نزد. آنها نارگیل های باقی مانده را به سه قسمت مساوی کردند و به هر یک 7 نارگیل رسید و 1 نارگیل هم اضافه آمد که ان را برای میمون ها انداختند. حال شما بگویید که در ابتدا ملوان ها چند نارگیل جمع آوری کردند؟ |
پاسخ این مسئله 79 نارگیل است. برای حل، ابتدا از راهبرد بزیر مساله به همان ترتیب از آخر به اول استفاده کنید اما همزمان راهبرد رسم شکل را نیز بکار برید.
این مسئله را می توان به شکل دیگری نیز مطرح کرد یعنی بجای اینکه بگوییم “ در پایان ، تعداد نارگیل های باقیمانده را که قسمت کردند به هر ملوان 7 نارگیل رسید و 1 نارگیل برای میمون ها باقی ماند“ بگوییم “ در پایان تعداد نارگیل های باقیمانده ، بطور مساوی بین سه ملوان قسمت شد و 1 نارگیل برای میمون ها باقی ماند“.
این کار باعث می شود تا دانش آموزان از راهبرد حدس و آزمایش هم استفاده کنند و برای تعداد نارگیل های هر ملوان حدس های مختلفی بزنند. البته آنها بسرعت می توانند حدس های غیر منطقی را حذف نمایند زیرا عدد پیشنهادی باید بر 3 قابل قسمت باشد تا بتواند بین 3 ملوان تقسیم گردد.
توسعه
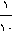 انبه ها را می خورد ، نفر دوم
انبه ها را می خورد ، نفر دوم  باقیمانده ، نفر سوم
باقیمانده ، نفر سوم 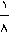 باقیمانده و بهمین ترتیب تا اینکه فقط 3 انبه باقی بماند .
باقیمانده و بهمین ترتیب تا اینکه فقط 3 انبه باقی بماند .